파인만은 강의 I에서 자연 현상 설명하기 위한 물리이론이 어떻게 진화되어 왔는가를 수학의 '양적' 기술 측면을 기막히게 활용하여, 알기쉽게 설명하였다, 모순되는 관찰로부터 받아들여야만 했던 로렌쯔 수축 => $E=mc^2$, cutoff 함수 => 플랑크 상수, 양자역학 등.
그리고 어김없이 기회마다 전자의 point particle 취급의 문제점, 전자파 resistance 등 여러 가설과 이론들이 smoothly 연결되지 않는 부분들을 솔직성을 담아 짚고 넘어갔다.
여기 이 짧막한 메모는, 파인만의 생각 흐름에 충실히 따라
그 원인이 양적 계산에 치중하고 '기학하적' 구조를 고려하지 않은 결과임을 색깔 분류 등 예로 입증한다.

1. 입자에 대한 관점
직관 요점적으로 얘기하면
우리가 보고 느끼는 3차원 세상은 고차원 projection이고, 입자의 이중성, 편광이란 것들은 장님 코끼리 만지듯이, 어느 한 측면으로만 보고 논한 것에 지나지 않는다 거.
태양 주위를 도는 지구 궤도가 한 평면에 있지 않듯이, 빛의 동선은 4차원 다양체에서 노는 action*, 동양에서 '기(氣)'라고 부르는 모였다 흩어졌다 하지만 never disappear하는 움직임들의 flow, 그 flow가 만드는 기하학적 구조 측면을 보아야 한다는 거다
* 에너지, 움직임, 기와 같은 의미로 혼용

% 기들이 만드는 다양체를 위한 참조 영상들
물고기 떼들이 만드는 입체(물고기를 氣로 보고)

이러한 관점에 들어맞는 법칙과 파인만의 암시적인 묘사들
(1) 에너지, 운동량 등의 보존 법칙들
(2) 스크린에 그림 그리는 화가
(3) 다른 차원 넘나드는 빛
(4) polarization 등

2. 색깔: 빛이 3개의 orientable 4차원 다양체, $CP^2, S^2\times S^2$와 $S_t$(= the orientable twisted $S^2$ bundle over $S^2$) 위에서 흐르는 움직임들, 즉 sensation

섯다나 포카에서 패를 쪼며 원하는 패가 들어왔음을 보았을 때 짜릿함, 소름 끼쳤을 때 뭔가 등을 타고 흐르는 걸 느낀다, 그리고 그 sensation... 뭔가 흐르는 그 움직임들이, 상황에 따라 만드는 경로 등 어딘지 모르게 다르다는 걸 감으로 안다.
여기서 얘기하고자 하는 것이 그 경로가 만드는 기하하적 구조와 색깔이 만드는 sensation의 연관 대응성이다, intuitively.

(1) 빛은 맥스웰 방정식에 의하여 전자기 $E, B$ 2개의 circular action, 즉 $T^2=S^1\times S^1$ 액션을 갖는데, 파인만은 그 중 하나인 전기장의 circular action의 projected된 근사식 $E(t)={\text{상수}}\times \cos(\omega(t-r/c)+\phi)$로
 
간섭, 굴절, 편광 등 빛의 많은 현상을 성공적으로 설명하였다.
이와 같은 접근 방법으로 투사된 것을 1개 => 2개 action들로 넓혀 들여다 보면

(2) 눈에 투사된 빛의 data 표현, 4차원 다양체 $M$의 orbit space $M/{T^2}$와 그 분류

① 인간은 3차원에 살고 있지만 눈에 투사되는 것은 2차원이고 거기에 투사, 즉 포개진 $E, B$ action 정보들 포함한 것을 수학적으로 표현하면 아래와 같은 원판들 모임이고

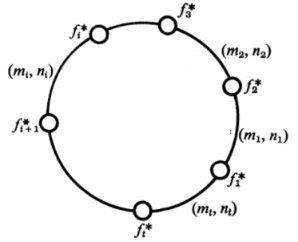
옆의 표시들은 투사/포개진 정도를 나타내는 $T^2$의 subgroup들로서 1. $f^*_i$: $T^2$에 의해 고정 즉 움직이지 않는 점 2. $(m_i, n_i)$: circle subgroup 3. 원판 내부는 포개지는 것이 없는 부분 * 자세한 것은 참고 문헌 2

② 느끼는 sensation은, 위 원판 정보들이 육체에 갇혀있거나 매어있는 움직임들에 의해 재현된 것으로, 수학적 표현으로 blowup된 그 4차원 manifold들은 Orlik과 Raymond에 의하면(참고 문헌 2),
1) $CP^2, S^2\times S^2$, $S_t$의 합으로 equivarianly(물리적으로 resonantly) 분류되고
2) $-CP^2$($CP^2$ with reverse orientation) 포함되어 있다는 거
3) $CP^2\#(-CP^2)\#CP^2$=$S^2\times S^2\#CP^2$처럼 connected sum이 유일하지 않단다
이는

(3) $R, G, B$(빨강, 녹색, 파랑)의 색 조합 실험에 의하면
① 모든 색은 수학적인 $aR+bG+cB$으로 표할 수 있고
② a, b, c 중 하나는 반드시 음수이어야 한다는 것
③ 색을 만드는 조합이 유일하지 않다는 것과 기막히게 대응된다

% 대응 비교표

움직임들이 만드는 4차원 다양체	색깔
$CP^2, S^2\times S^2$, $S_t$	빨강 R, 녹색 G, 파랑 B
$aCP^2\#bS^2\times S^2 \#cS_t$	$aR+bG+cB$
$-CP^2$, $-$ 는 거꾸로 도는 것으로 에너지 감소	a,b,c 중 하나는 반드시 음수
유일하지 않은 connected sum	유일하지 않은 색 조합
equivariantly, 같게 변화	resonantly, 같은 자극

3. 그 밖에
새로운 입자 관점을 적용해보면

(1) 원자의 angular momentum
리튬은 spin of three-halves, 전자 3개를 갖는다고 한다. 전자가 움직이며 만드는 4차원 다양체를 $CP^2$라고 하면, 리튬의 앵귤라 모멘텀이 간단히 설명된다. 다시 말해서, $CP^2$와 $-CP^2$ 조합으로
$3CP^2$, $CP^2$+$CP^2$+$-CP^2$=$CP^2$, $CP^2$+$-CP^2$+$-CP^2$=$-CP^2$, $-CP^2$+$-CP^2$+$-CP^2$=$-3CP^2$ $CP^2$에 $\frac12$대입하면, $\frac32, \frac12, -\frac12, -\frac32$

(2) meson의 2가지 분해
실험 수치상 같은 입자로 추정되는데, 2가지 다른 방법으로 disintegrate 분해되는 $\theta, \tau$ 메손이 있다고 한다. 이것 또한 action 다양체의 connected sum이 유일하지 않다는 것으로 이해될 수 있다.
덧붙여, $S_t$와 $CP^2\#-CP^2$ topologically 같다. 좀 더 자세히 말하면, $S_t$ is diffeomorphic $CP^2\#-CP^2$, but not always equivariantly diffeomorphic(참조 문헌 2).

참고 문헌
1. The Feynman Lectures on Physics, Volume I
2. P. Orlik and F. Raymond, Actions of the torus on 4-manifols I